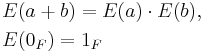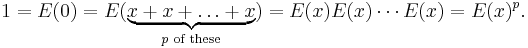Exponential field

In mathematics, an exponential field is a field that has an extra operation on its elements which extends the usual idea of exponentiation.

1 Definition
2 Examples
3 Open problems
4 See also
5 Notes

Definition

A field is an algebraic structure composed of a set of elements, F, and two operations, addition ('+') and multiplication ('·'), such that the set of elements forms an abelian group under both operations with identities 0_F and 1_F respectively, and such that multiplication is distributive over addition, that is for any elements a, b, c in F, one has a · (b + c) = (a · b) + (a · c). If there is also a function E that maps F into F, and such that for every a and b in F one has

$\begin{align}&E(a%2Bb)=E(a)\cdot E(b),\\ &E(0_F)=1_F \end{align}$

then F is called an exponential field, and the function E is called an exponential function on F.^[1] Thus an exponential function on a field is a homomorphism from the additive group of F to its multiplicative group.

Examples

There is a trivial exponential function on any field, that is the map E that sends every element to 1_F, the identity element of the field under multiplication. Thus every field is trivially also an exponential field, so the cases of interest to mathematicians occur when the exponential function is non-trivial.

If a field has characteristic p > 0 then it can be shown that the only exponential function on the field is the trivial one.^[2] To see this first note that for any element x in the field,

$1=E(0)=E(\underbrace{x%2Bx%2B\ldots%2Bx}_{p\text{ of these}})=E(x)E(x)\cdots E(x)=E(x)^p.$

Hence, taking into account the Frobenius endomorphism,

$(E(x)-1)^p=E(x)^p-1^p=E(x)^p-1=0.\,$

And so E(x) = 1 for every x. For this reason, exponential fields are sometimes required to have characteristic zero.^[3]

When the field does have characteristic zero then there can be non-trivial exponential functions.

The field of real numbers R, or (R,+,·,0,1) as it may be written to highlight that we are considering it purely as a field with addition, multiplication, and special constants zero and one, has infinitely many exponential functions. One such function is the usual exponential function, that is E(x) = e^x, since we have e^x+y = e^xe^y and e⁰ = 1, as required. Considering the ordered field R equipped with this function gives the ordered real exponential field, denoted R_exp = (R,+,·,<,0,1,exp).

In fact any real number a > 0 gives an exponential function on R, specifically the map E(x) = a^x satisfies the required properties.

Analogously to the real exponential field, there is the complex exponential field, C_exp = (C,+,·,0,1,exp).

Boris Zilber constructed an exponential field K_exp that, crucially, satisfies the equivalent formulation of Schanuel's conjecture with the field's exponential function.^[4] It is conjectured that this exponential field is actually C_exp, and a proof of this fact would thus prove Schanuel's conjecture.

The underlying set F may not be required to be a field but instead allowed to simply be a ring, R, and concurrently the exponential function is relaxed to be a homomorphism from the additive group in R to the multiplicative group of units in R. The resulting object is called an exponential ring.^[2]

An example of an exponential ring with a nontrivial exponential function is the ring of integers Z equipped with the function E which takes the value +1 at even integers and −1 at odd integers, i.e., the function 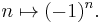$n \mapsto (-1)^n.$ This exponential function, and the trivial one, are the only two functions on Z that satisfy the conditions.^[5]

Open problems

Exponential fields are a much-studied object in model theory, occasionally providing a link between it and number theory as in the case of Zilber's work on Schanuel's conjecture. It was proved in the 1990s that R_exp is model complete, a result known as Wilkie's theorem. This result, when combined with Khovanskiĭ's theorem on pfaffian functions, proves that R_exp is also o-minimal.^[6] On the other hand it is known that C_exp is not model complete.^[7] The question of decidability is still unresolved. Alfred Tarski posed the question of the decidability of R_exp and hence it is now known as Tarski's exponential function problem. It is known that if the real version of Schanuel's conjecture is true then R_exp is decidable.^[8]

Notes

^ Helmut Wolter, Some results about exponential fields (survey), Mémoires de la S.M.F. 2^e série, 16, (1984), pp.85–94.
^ ^a ^b Lou van den Dries, Exponential rings, exponential polynomials and exponential functions, Pacific Journal of Mathematics, 113, no.1 (1984), pp.51–66.
^ Martin Bays, Jonathan Kirby, A.J. Wilkie, A Schanuel property for exponentially transcendental powers, (2008), arXiv:0810.4457
^ Boris Zilber, Pseudo-exponentiation on algebraically closed fields of characteristic zero, Ann. Pure Appl. Logic, 132, no.1 (2005), pp.67–95.
^ Giuseppina Terzo, Some Consequences of Schanuel's Conjecture in Exponential Rings, Communications in Algebra, Volume 36, Issue 3 (2008), pp.1171–1189.
^ A.J. Wilkie, Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function, J. Amer. Math. Soc., 9 (1996), pp.1051–1094.
^ David Marker, A remark on Zilber's pseudoexponentiation, The Journal of Symbolic Logic, 71, no.3 (2006), pp.791–798.
^ A.J. Macintyre, A.J. Wilkie, On the decidability of the real exponential field, Kreisel 70th Birthday Volume, (2005).

Exponential field

Contents

Definition

Examples

Open problems

See also

Notes